Sıralama Algoritmaları – Merge Sort (Birleştirme Sıralaması) Algoritması

Bu yazımızda merge sort (birleştirme sıralaması) algoritması hakkında bilgiler vereceğiz.

Merge Sort (Birleştirme Sıralaması) Algoritması Nedir ?

Merge Sort, verileri bölme ve birleştirme yöntemi kullanarak sıralama işlemini gerçekleştirir. İlk olarak, veriler belirli bir noktadan bölünür ve her bir bölüm ayrı ayrı sıralanır. Bölme işlemi verilerin en küçük birimine kadar devam eder. Sonra, sıralı olan veriler tekrar birleştirilir ve böylece veriler tamamen sıralı hale gelir.

Bu algoritmanın avantajı, verileri sıralarken her bir verinin tek tek ele alınmasıdır. Bu sayede veriler doğru bir şekilde sıralanır ve algoritmanın güvenilirliği artar. Ayrıca, verilerin bölünmesi ve tekrar birleştirilmesi işlemi paralelleştirilebilir, böylece sıralama işlemi daha hızlı gerçekleştirilebilir.

Eksi yönleri ise, verilerin bölünmesi ve birleştirilmesi sırasında ekstra bellek alanı gerektirmesi ve sıralama işlemi için ekstra zaman gerektirmesidir. Ancak, veriler büyükse ve sıralama işlemi öncelikli ise, Merge Sort tercih edilebilir.

Merge Sort (Birleştirme Sıralaması) Algoritması Nasıl Çalışır ?

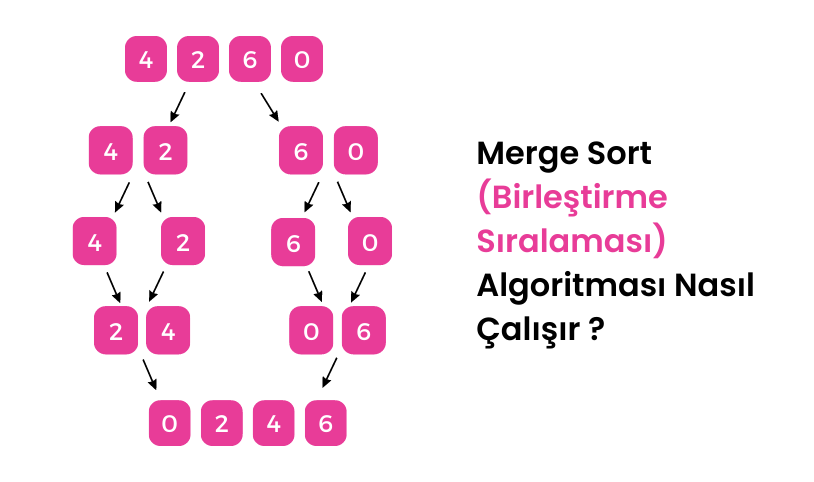
Merge Sort algoritması, verileri sıralamak için böl-ve-yönet yöntemini kullanır. Aşağıdaki adımları içerir:

1. Veriler bölünür: Veriler belirli bir noktadan bölünür ve her bir bölüm ayrı ayrı sıralanır. Bölme işlemi verilerin en küçük birimine kadar devam eder.
2. Veriler sıralanır: Her bir veri bölümü ayrı ayrı sıralanır. Sıralama işlemi, verilerin en küçükten en büyüğe doğru dizilmesidir.
3. Veriler birleştirilir: Sıralı olan veriler tekrar birleştirilir ve böylece veriler tamamen sıralı hale gelir. Birleştirme işlemi, iki sıralı veri bölümünü karşılaştırarak, sıralı bir şekilde birleştirilmesini sağlar.

Bu adımlar tekrar edilir ve veriler tamamen sıralı hale gelene kadar devam eder. Bu algoritma, verileri doğru bir şekilde sıralamayı garanti eder ve genellikle hızlı bir şekilde çalışır.

Merge Sort (Birleştirme Sıralaması) Algoritması Zaman Karmaşıklığı

Merge Sort algoritmasının zaman karmaşıklığı O(n * log(n)) dir. Bu, verilerin bölünmesi ve birleştirilmesi sırasında yapılan işlem sayısı ile orantılıdır. Her bir bölüm sıralandıktan sonra, veriler tekrar birleştirilir ve bu işlem logaritmik bir zaman gerektirir. Böylece, verilerin boyutu büyüdükçe işlem sayısı da artar, ancak logaritmik bir şekilde artar ve zaman karmaşıklığı O(n * log(n)) olarak kalır.

Merge Sort (Birleştirme Sıralaması) Algoritması Örnek Kod

Şimdide örnek olması açısında c programlama dilinde yazılımış bir merge sort örneğini görelim.

#include <stdio.h>

void merge(int arr[], int l, int m, int r)
{
    int i, j, k;
    int n1 = m - l + 1;
    int n2 = r - m;
 
    int L[n1], R[n2];
 
    for (i = 0; i < n1; i++)
        L[i] = arr[l + i];
    for (j = 0; j < n2; j++)
        R[j] = arr[m + 1 + j];
 
    i = 0;
    j = 0;
    k = l;
    while (i < n1 && j < n2)
    {
        if (L[i] <= R[j])
        {
            arr[k] = L[i];
            i++;
        }
        else
        {
            arr[k] = R[j];
            j++;
        }
        k++;
    }
 
    while (i < n1)
    {
        arr[k] = L[i];
        i++;
        k++;
    }
 
    while (j < n2)
    {
        arr[k] = R[j];
        j++;
        k++;
    }
}
 
void mergeSort(int arr[], int l, int r)
{
    if (l < r)
    {
        int m = l + (r - l) / 2;
 
        mergeSort(arr, l, m);
        mergeSort(arr, m + 1, r);
 
        merge(arr, l, m, r);
    }
}
 
int main()
{
    int arr[] = {12, 11, 13, 5, 6, 7};
    int arr_size = sizeof(arr) / sizeof(arr[0]);
 
    printf("Given array is \n");
    for (int i=0; i < arr_size; i++)
        printf("%d ", arr[i]);
 
    mergeSort(arr, 0, arr_size - 1);
 
    printf("\nSorted array is \n");
    for (int i=0; i < arr_size; i++)
        printf("%d ", arr[i]);
    return 0;
}

Çıktısı :

Given array is 
12 11 13 5 6 7 
Sorted array is 
5 6 7 11 12 13

Bu yazımızda merge sort (birleştirme sıralaması) algoritması hakkında bilgiler verdik. Diğer veri yapıları konulu yazılarımızı okumak için buraya tıklayabilirsiniz.